tl;dr

• Multiplying the middle element of 3x3 matrix with 9 gets thesum of all elements.
• Adding the least element of 5x4 matrix with the larget and multiplying this result by 10 gets the sum of all elements.
• multiplying any row with 2000 and subtrating that number by 2 will get you the sum.
• Remaing two rows can be filled with the result of subtracting 9 from each digit of a corresponding row .

tl;dr

• Create a Linux profile for Ubuntu 18.04 (5.4.0-42-generic) in Volatility
• Use linux_bash plugin to get link to the repo and linux_find_file plugin to recover the filepath
• Decode the keyboard stream data to retrieve the flag

tl;dr

• This is a fairly simple Maze challenge
• Challenge is written in rust

Challenge author: Freakston, silverf3lix

Descrption

Senpai plis find me a way.

Solution

This is a fairly simple maze challenge implemented in rust.

At the start of the main function of the challenge miz we can see there is a some sort of a initialization going on at a function named miz::bacharu::Kikai::new::h3a113b790cc2bb5c

We can see from here than this function takes care of initializing the maze. We can extract the maze bytes either directly from here or during runtime, which ever is preferred.

Moving forward we can see that the function is also getting our input, and sending it over to another function miz::bacharu::Kikai::run::h14398f1fc265e61e

The function miz::bacharu::Kikai::run takes care of the maze logic, the up, left, down and right.

• Case “h”

We can see that the case “h” takes care of going left, which is by subtracting 1 from the y coordinate

• Case “j”

Similarly, case “j” is to go up, it does this by subtracting 1 from the x coordinate.

• Case “k”

Case “k” takes care of going down the maze, it adds 1 to the x coordinate

• Case “l”

This case takes care of going right in the maze, it does so by adding 1 to the y coordinate

From this function we can also get the bounds of the maze which is 24 x 25, where there are 25 rows and 24 columns.

And the properties of the maze are,

• “0” ⇒ Path to traverse
• “1” ⇒ Walls
• “2” ⇒ Final win position

We can also see that this is the function miz::bacharu::Kikai::Furagu_o_toru::hd3e3c2fb2ccf3552 is the win function, and this is called when we traverse till we reach the number 2 in the maze.

Constructing the maze should be easy since we have its bounds,

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

miz =       [[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
            ,[1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,1]
            ,[1,0,1,0,1,1,1,1,1,1,1,1,1,1,1,0,1,0,1,1,1,0,1,0,1]
            ,[1,0,1,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,1,0,0,0,1]
            ,[1,0,1,1,1,1,1,1,1,0,1,0,1,1,1,1,1,1,1,0,1,1,1,1,1]
            ,[1,0,0,0,0,0,0,0,1,0,1,0,0,0,1,0,0,0,0,0,1,0,0,0,1]
            ,[1,0,1,1,1,1,1,0,1,1,1,0,1,0,1,1,1,0,1,1,1,1,1,0,1]
            ,[1,0,0,0,1,0,1,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1]
            ,[1,1,1,0,1,0,1,0,1,1,1,1,1,1,1,0,1,1,1,0,1,0,1,1,1]
            ,[1,0,1,0,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,1]
            ,[1,0,1,0,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1]
            ,[1,0,1,0,1,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,1]
            ,[1,0,1,0,1,0,1,1,1,0,1,1,1,1,1,0,1,0,1,0,1,0,1,0,1]
            ,[1,0,0,0,1,0,0,0,1,0,0,0,1,0,1,0,0,0,1,0,0,0,1,0,1]
            ,[1,0,1,1,1,1,1,1,1,1,1,0,1,0,1,1,1,1,1,1,1,1,1,0,1]
            ,[1,0,0,0,1,0,0,0,0,0,0,0,1,0,1,0,0,0,1,0,0,0,0,0,1]
            ,[1,0,1,0,1,0,1,1,1,1,1,1,1,0,1,0,1,1,1,0,1,1,1,0,1]
            ,[1,0,1,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,1,0,1,0,1,0,1]
            ,[1,0,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,0,1,0,1,0,1,0,1]
            ,[1,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,1]
            ,[1,0,1,1,1,1,1,1,1,1,1,1,1,0,1,0,1,1,1,1,1,0,1,0,1]
            ,[1,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,1,0,0,0,1,0,1,0,1]
            ,[1,1,1,0,1,0,1,1,1,0,1,1,1,1,1,0,1,0,1,0,1,0,1,0,1]
            ,[1,0,0,0,1,0,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,1]
            ,[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,1,1,1,1,1]]

The start position can be retrieved while debugging and it is (0, 13). The end position is

(24, 19)

Final script

To solve this maze we can make use of the python library mazelib

Here is the script,

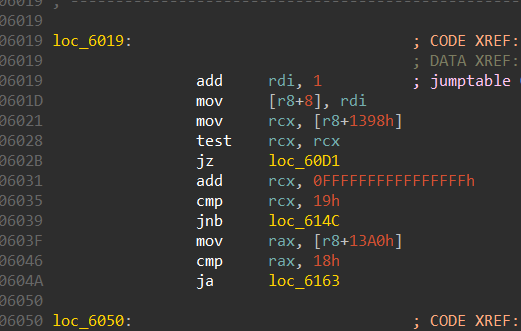
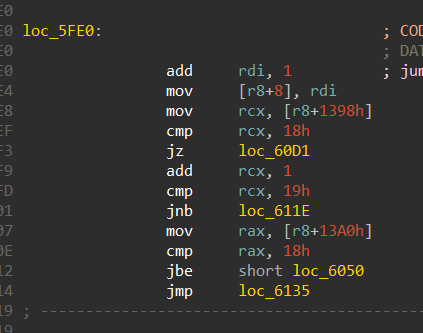
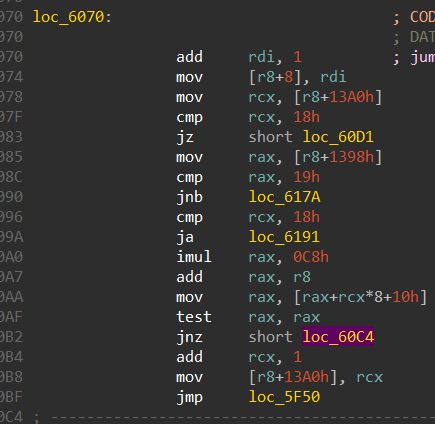
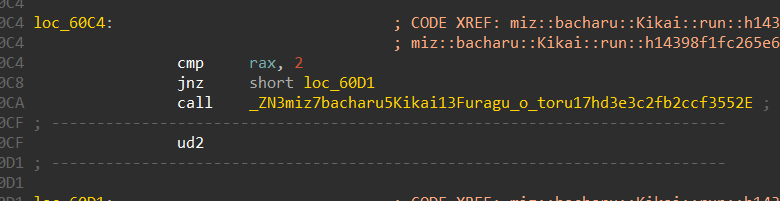
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

from mazelib import Maze
from mazelib.solve.BacktrackingSolver import BacktrackingSolver
import numpy as np
m = Maze()
m.solver = BacktrackingSolver()
miz =       [[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
            ,[1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,1]
            ,[1,0,1,0,1,1,1,1,1,1,1,1,1,1,1,0,1,0,1,1,1,0,1,0,1]
            ,[1,0,1,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,1,0,0,0,1]
            ,[1,0,1,1,1,1,1,1,1,0,1,0,1,1,1,1,1,1,1,0,1,1,1,1,1]
            ,[1,0,0,0,0,0,0,0,1,0,1,0,0,0,1,0,0,0,0,0,1,0,0,0,1]
            ,[1,0,1,1,1,1,1,0,1,1,1,0,1,0,1,1,1,0,1,1,1,1,1,0,1]
            ,[1,0,0,0,1,0,1,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1]
            ,[1,1,1,0,1,0,1,0,1,1,1,1,1,1,1,0,1,1,1,0,1,0,1,1,1]
            ,[1,0,1,0,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,1]
            ,[1,0,1,0,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1]
            ,[1,0,1,0,1,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,1]
            ,[1,0,1,0,1,0,1,1,1,0,1,1,1,1,1,0,1,0,1,0,1,0,1,0,1]
            ,[1,0,0,0,1,0,0,0,1,0,0,0,1,0,1,0,0,0,1,0,0,0,1,0,1]
            ,[1,0,1,1,1,1,1,1,1,1,1,0,1,0,1,1,1,1,1,1,1,1,1,0,1]
            ,[1,0,0,0,1,0,0,0,0,0,0,0,1,0,1,0,0,0,1,0,0,0,0,0,1]
            ,[1,0,1,0,1,0,1,1,1,1,1,1,1,0,1,0,1,1,1,0,1,1,1,0,1]
            ,[1,0,1,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,1,0,1,0,1,0,1]
            ,[1,0,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,0,1,0,1,0,1,0,1]
            ,[1,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,1]
            ,[1,0,1,1,1,1,1,1,1,1,1,1,1,0,1,0,1,1,1,1,1,0,1,0,1]
            ,[1,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,1,0,0,0,1,0,1,0,1]
            ,[1,1,1,0,1,0,1,1,1,0,1,1,1,1,1,0,1,0,1,0,1,0,1,0,1]
            ,[1,0,0,0,1,0,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,1]
            ,[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]]
m.grid = np.array(miz)
m.start = (0,13)
m.end = (24,19)
m.solve()
sol = m.solutions[0]

for i in range(len(sol)-1):
    x = sol[i][0]
    y = sol[i][1]
    xn = sol[i+1][0]
    yn = sol[i+1][1]
    #print(f"x -> {x} y- >{y}  xn -> {xn} yn -> {yn}")
    if (x - xn) > 0:
        print("j",end="")
    elif (y - yn) > 0:
        print("h",end="")
    elif (yn - y) > 0:
        print("l",end="")
    elif (xn - x) > 0:
        print("k",end="")

The final moves to be sent as input comes out to be,

llkkhhhhkkkkhhhhjjhhhhhhkkllkkkkkkhhkkllkklljjlllllljjhhjjllllllkklljjllkklljjllkkkkhhhhkkkkllkkkkhh

Flag: inctf{mizes_are_fun_or_get}

tl;dr

• Race condition to change the type.
• Leak using uninitialized memory and get rip with overflow.

tl;dr

• Heap Overflow in glob function while handling Tilde operator.
• Abuse null byte overflow to gain RCE.

tl;dr

• Use the integer overflow to trigger a kernel heap overflow.
• Use the heap overflow to overwrite tty structure function pointers to get code execution.

tl;dr

• Extract creation timestamp of a note from Google Keep Notes.
• Finding location, date & time from Slack Messages.
• Extract no. of tasks completed and created from Google Tasks.
• Finding secret code from Google Docs cache.
• Extract first opened timestamp of a Game.

tl;dr

• Extract User ID and Workspace ID of the Slack workspace participating.
• Extract the first & last 3 characters of text from the Anydesk Remote connected PC’s thumbnail wallpaper.
• Extract the type of filesystem of the USBs connected to the system.
• Extracting active duration of Voice Modulator application used by parsing Windows Activity timeline.

tl;dr

• Finding default browser and the top visited website.
• Extract timestamp, ID, Hostname of the TeamViewer FileTransfer session.

tl;dr

• Finding Chat application
• Extract unread message count from NTUSER.dat.
• Extract the last executed timestamp of the chat application.
• Extract the Version of the chat application.