tl;dr

  • This is a fairly simple Maze challenge
  • Challenge is written in rust

Challenge author: Freakston, silverf3lix

Descrption

Senpai plis find me a way.

Solution

This is a fairly simple maze challenge implemented in rust.

At the start of the main function of the challenge miz we can see there is a some sort of a initialization going on at a function named miz::bacharu::Kikai::new::h3a113b790cc2bb5c

We can see from here than this function takes care of initializing the maze. We can extract the maze bytes either directly from here or during runtime, which ever is preferred.

Moving forward we can see that the function is also getting our input, and sending it over to another function miz::bacharu::Kikai::run::h14398f1fc265e61e

The function miz::bacharu::Kikai::run takes care of the maze logic, the up, left, down and right.

  • Case “h”

We can see that the case “h” takes care of going left, which is by subtracting 1 from the y coordinate

  • Case “j”

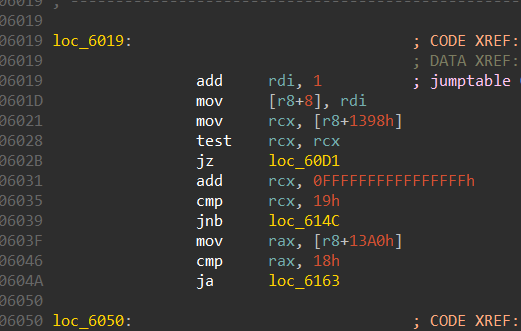
Similarly, case “j” is to go up, it does this by subtracting 1 from the x coordinate.

  • Case “k”

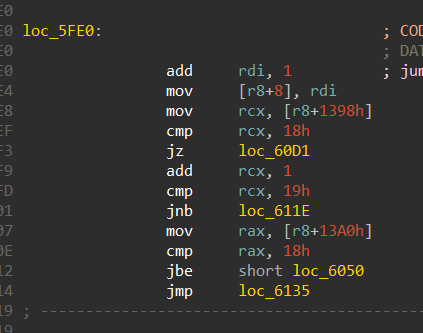
Case “k” takes care of going down the maze, it adds 1 to the x coordinate

  • Case “l”

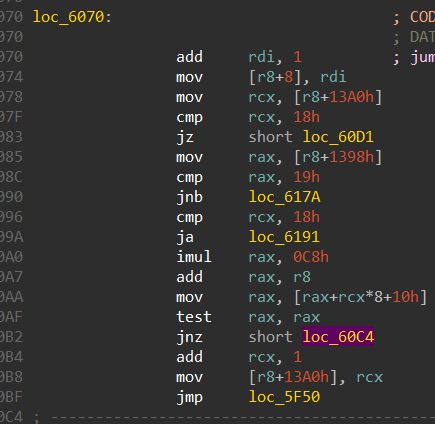
This case takes care of going right in the maze, it does so by adding 1 to the y coordinate

From this function we can also get the bounds of the maze which is 24 x 25, where there are 25 rows and 24 columns.

And the properties of the maze are,

  • “0” ⇒ Path to traverse
  • “1” ⇒ Walls
  • “2” ⇒ Final win position

We can also see that this is the function miz::bacharu::Kikai::Furagu_o_toru::hd3e3c2fb2ccf3552 is the win function, and this is called when we traverse till we reach the number 2 in the maze.

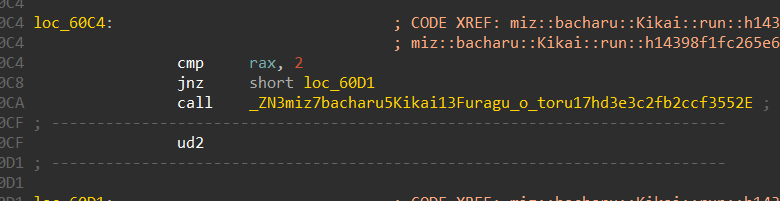
Constructing the maze should be easy since we have its bounds,

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
miz =       [[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
            ,[1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,1]
            ,[1,0,1,0,1,1,1,1,1,1,1,1,1,1,1,0,1,0,1,1,1,0,1,0,1]
            ,[1,0,1,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,1,0,0,0,1]
            ,[1,0,1,1,1,1,1,1,1,0,1,0,1,1,1,1,1,1,1,0,1,1,1,1,1]
            ,[1,0,0,0,0,0,0,0,1,0,1,0,0,0,1,0,0,0,0,0,1,0,0,0,1]
            ,[1,0,1,1,1,1,1,0,1,1,1,0,1,0,1,1,1,0,1,1,1,1,1,0,1]
            ,[1,0,0,0,1,0,1,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1]
            ,[1,1,1,0,1,0,1,0,1,1,1,1,1,1,1,0,1,1,1,0,1,0,1,1,1]
            ,[1,0,1,0,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,1]
            ,[1,0,1,0,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1]
            ,[1,0,1,0,1,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,1]
            ,[1,0,1,0,1,0,1,1,1,0,1,1,1,1,1,0,1,0,1,0,1,0,1,0,1]
            ,[1,0,0,0,1,0,0,0,1,0,0,0,1,0,1,0,0,0,1,0,0,0,1,0,1]
            ,[1,0,1,1,1,1,1,1,1,1,1,0,1,0,1,1,1,1,1,1,1,1,1,0,1]
            ,[1,0,0,0,1,0,0,0,0,0,0,0,1,0,1,0,0,0,1,0,0,0,0,0,1]
            ,[1,0,1,0,1,0,1,1,1,1,1,1,1,0,1,0,1,1,1,0,1,1,1,0,1]
            ,[1,0,1,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,1,0,1,0,1,0,1]
            ,[1,0,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,0,1,0,1,0,1,0,1]
            ,[1,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,1]
            ,[1,0,1,1,1,1,1,1,1,1,1,1,1,0,1,0,1,1,1,1,1,0,1,0,1]
            ,[1,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,1,0,0,0,1,0,1,0,1]
            ,[1,1,1,0,1,0,1,1,1,0,1,1,1,1,1,0,1,0,1,0,1,0,1,0,1]
            ,[1,0,0,0,1,0,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,1]
            ,[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,1,1,1,1,1]]

The start position can be retrieved while debugging and it is (0, 13). The end position is

(24, 19)

Final script

To solve this maze we can make use of the python library mazelib

Here is the script,

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
from mazelib import Maze
from mazelib.solve.BacktrackingSolver import BacktrackingSolver
import numpy as np
m = Maze()
m.solver = BacktrackingSolver()
miz =       [[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
            ,[1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,1]
            ,[1,0,1,0,1,1,1,1,1,1,1,1,1,1,1,0,1,0,1,1,1,0,1,0,1]
            ,[1,0,1,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,1,0,0,0,1]
            ,[1,0,1,1,1,1,1,1,1,0,1,0,1,1,1,1,1,1,1,0,1,1,1,1,1]
            ,[1,0,0,0,0,0,0,0,1,0,1,0,0,0,1,0,0,0,0,0,1,0,0,0,1]
            ,[1,0,1,1,1,1,1,0,1,1,1,0,1,0,1,1,1,0,1,1,1,1,1,0,1]
            ,[1,0,0,0,1,0,1,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1]
            ,[1,1,1,0,1,0,1,0,1,1,1,1,1,1,1,0,1,1,1,0,1,0,1,1,1]
            ,[1,0,1,0,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,1]
            ,[1,0,1,0,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1]
            ,[1,0,1,0,1,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,1]
            ,[1,0,1,0,1,0,1,1,1,0,1,1,1,1,1,0,1,0,1,0,1,0,1,0,1]
            ,[1,0,0,0,1,0,0,0,1,0,0,0,1,0,1,0,0,0,1,0,0,0,1,0,1]
            ,[1,0,1,1,1,1,1,1,1,1,1,0,1,0,1,1,1,1,1,1,1,1,1,0,1]
            ,[1,0,0,0,1,0,0,0,0,0,0,0,1,0,1,0,0,0,1,0,0,0,0,0,1]
            ,[1,0,1,0,1,0,1,1,1,1,1,1,1,0,1,0,1,1,1,0,1,1,1,0,1]
            ,[1,0,1,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,1,0,1,0,1,0,1]
            ,[1,0,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,0,1,0,1,0,1,0,1]
            ,[1,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,1]
            ,[1,0,1,1,1,1,1,1,1,1,1,1,1,0,1,0,1,1,1,1,1,0,1,0,1]
            ,[1,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,1,0,0,0,1,0,1,0,1]
            ,[1,1,1,0,1,0,1,1,1,0,1,1,1,1,1,0,1,0,1,0,1,0,1,0,1]
            ,[1,0,0,0,1,0,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,1]
            ,[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]]
m.grid = np.array(miz)
m.start = (0,13)
m.end = (24,19)
m.solve()
sol = m.solutions[0]

for i in range(len(sol)-1):
    x = sol[i][0]
    y = sol[i][1]
    xn = sol[i+1][0]
    yn = sol[i+1][1]
    #print(f"x -> {x} y- >{y}  xn -> {xn} yn -> {yn}")
    if (x - xn) > 0:
        print("j",end="")
    elif (y - yn) > 0:
        print("h",end="")
    elif (yn - y) > 0:
        print("l",end="")
    elif (xn - x) > 0:
        print("k",end="")

The final moves to be sent as input comes out to be,

llkkhhhhkkkkhhhhjjhhhhhhkkllkkkkkkhhkkllkklljjlllllljjhhjjllllllkklljjllkklljjllkkkkhhhhkkkkllkkkkhh

Flag: inctf{mizes_are_fun_or_get}

InCTFi Linux Reversing Maze Rust

tl;dr

  • This is a simple stack based VM
  • 25-27 opcodes and 8 different constraints
  • Extract the constraints
  • Use z3 to find a satisfying model

Challenge Points: 245
Challenge Solves: 20
Challenge author: EvilMuffinHa
Solved by: AmunRha, Freakston, barlabhi

Description

Introduction

This is a simple VM which has around 25-27 opcodes with instructions simple enough to be emulated. This is a stack based VM.

The VM implements several constraints on the input bytes which can be solved using z3 SMT solver.

The VM implemented a puzzle called kenken

Solution

I chose python to write the disassembler in with several helper functions, at first I tried extracting the constrains one by one, which eventually worked, but then I was able to write a automatic extractor for the disassembly.

There were two files, one the binary and the data file in which the list of instructions contain.

This when fed to the z3 solution script will get us the required input.

Most of the operations take their operands from the stack, so there wasn’t much complexity in terms of implementation.

p.s. This will be a short write up

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
def disasm(op, c):
    if c > dump_len:
        return -1
    # print(f"\n[{hex(op):<3}]:[{hex(c):<3}]\t")
    # print("MOV dctr, ctr1+1")
    # print(op_desc[op]+'\n')
    extract(op,rsp,ctr1)

    dctr = ctr1 + 1
    if op == 0x1:
        rsp.append(rsp[-1])
        ctr1+=1
    elif op == 0x2:
        rsp = rsp[:-1]
        ctr1+=1   
    elif op == 0x3:
        if rsp[-1] == -1:
            rsp = rsp[:-1]
            ctr1+=1
        elif rsp[-1] != 0:
            print(f"[+] RETURN: {rsp[-1]}")
            return -1
        else:
            print("[+] READING FLAG FILE")
            return 1
    elif op == 0x10:
        rsp[-2] = rsp[-1] + rsp[-2]
        rsp = rsp[:-1]
        ctr1+=1    
    elif op == 0x11:
        rsp[-2] = rsp[-1] - rsp[-2]
        rsp = rsp[:-1]
        ctr1+=1   
    elif op == 0x12:
        rsp[-2] = rsp[-1] * rsp[-2]
        rsp = rsp[:-1]
        ctr1+=1     
    elif op == 0x13:
        rsp[-2] = rsp[-1] // rsp[-2]
        rsp = rsp[:-1]
        ctr1+=1    
    elif op == 0x14:
        rsp[-2] = rsp[-1] % rsp[-2]
        rsp = rsp[:-1]
        ctr1+=1   
    elif op == 0x15:
        tmp = rsp[-1]
        rsp.pop(-1)
        res = rsp[-2]*rsp[-1]%tmp
        rsp = rsp[:-2]
        rsp.append(res)
        ctr1 = dctr  
    elif op == 0x16:
        rsp[-2] = 1 if rsp[-1] == rsp[-2] else 0
        ctr1+=1
        rsp = rsp[:-1]    
    elif op == 0x17:
        if rsp[-1] < 0:
            rsp[-1] = -1
        elif rsp[-1] > 0:
            rsp[-1] = 1
        ctr1+=1   
    elif op == 0x20:
        rsp.append(inp[ii])
        ii+=1
        ctr1 = dctr  
    elif op == 0x21:
        v30 = rsp[-1]
        rsp = rsp[:-1]
        ctr1 = dctr
        print(chr(v30))
        output.append(v30) 
    elif op == 0x22:
        ctr1+=3
        rsp.append((f[dctr+1]<<8) | f[dctr]) 
    elif op == 0x30:
        v30 = rsp.pop(-1)
        ctr1 = abs(v30)  
    elif op == 0x31:
        if rsp[-2] != 0:    #  Adjust/Remove the condition in order to extract
            rsp = rsp[:-2]  #  all equations with test input
            ctr1+=1         #  Keep it if using valid input
        else:
            ctr1 = rsp[-1]
            rsp = rsp[:-2]   
    elif op == 0x32:
        if rsp[-2] != 0:     #  Adjust/Remove the condition in order to extract
            ctr1 = rsp[-1]   #  all equations with test input
            rsp = rsp[:-2]   #  Keep it if using valid input
        else:
            rsp = rsp[:-2]
            ctr1+=1   
    elif op == 0x33:
        if rsp[-2] < 0:
            ctr1 = rsp[-1]
            rsp = rsp[:-2]
        else:
            rsp = rsp[:-2]
            ctr1+=1    
    elif op == 0x34:
        if rsp[-2] <= 0:
            rsp = rsp[:-2]
            ctr1+=1
        else:
            ctr1 = rsp[-1]
            rsp = rsp[-2]   
    elif op == 0x35:
        if rsp[-2] > 0:
            rsp = rsp[:-2]
            ctr1+=1
        else:
            ctr1 = rsp[-1]
            rsp = rsp[-2]    
    elif op == 0x36:
        if rsp[-2] >= 0:
            ctr1 = rsp[-1]
            rsp = rsp[:-2]
        else:
            rsp = rsp[:-2]
            ctr1+=1    
    elif op == 0x40:
        v33 = rsp.pop(-1)
        data[v13] = v33
        ctr1 = dctr    
    elif op == 0x41:
        ctr1+=1
        rsp.append(data[v13])   
    elif op == 0x50:
        v13+=1
        ctr1+=1   
    elif op == 0x51:
        v13-=1
        ctr1+=1    
    elif op == 0x52:
        v13 = (rsp[-1]+v13) & 0xff
        ctr1+=1
        rsp = rsp[:-1]    
    elif op == 0x53:
        v13 = (v13 - rsp[-1]) & 0xff
        ctr1+=1
        rsp = rsp[:-1]            
    else:
        print(f"""[!] UNKNOWN OPCODE: {hex(op)}""", end='')
        return -1

    # print_stack(rsp)
    # print_data(data)
    # print_reg(v13,ctr1,dctr,ii)
    return ctr1

Commenting the lines specified can get us the extracted constrains.

I wrote a small parser on my disassembly which will get the proper constraints.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
equations = {"add_2":[], "add_3":[], "equate_3": [], "equate_4":[], "mod_equate_2":[], "sub_2":[], "equal_2":[]}
def parse(bbl, f):
    PUSH_OPERAND = [0x22, 0x52, 0x41]
    SUB_2 = (16,2)
    EQUATE_3 = (21,3)
    EQUATE_4 = (28,4) 
    ADD_2 = (13,2)
    ADD_3 = (19,3)
    MOD_EQUATE_2 = (64,2)
    EQUAL_2 = (7,2)

    for llist in bbl:
        eq = []
        bbl_len = len(llist)
        i = 1
        while True:
            if i+2 >= bbl_len:
                break
            if [llist[i][0],llist[i+1][0],llist[i+2][0]] == PUSH_OPERAND:
                ctr = llist[i][1]
                res = f[ctr+1]
                eq.append(res)
                i+=3
            i+=1
        ctr = llist[0][1]
        res = [f[ctr+1]]
        if bbl_len == SUB_2[0]:
            eq = eq[:SUB_2[1]] + res
            equations["sub_2"].append(eq)
        elif bbl_len == EQUATE_3[0]:
            eq = eq[:EQUATE_3[1]] + res
            equations["equate_3"].append(eq)
        elif bbl_len == EQUATE_4[0]:
            eq = eq[:EQUATE_4[1]] + res
            equations["equate_4"].append(eq)
        elif bbl_len == ADD_2[0]:
            eq = eq[:ADD_2[1]] + res
            equations["add_2"].append(eq)
        elif bbl_len == ADD_3[0]:
            eq = eq[:ADD_3[1]] + res
            equations["add_3"].append(eq)
        elif bbl_len == MOD_EQUATE_2[0]:
            eq = eq[:MOD_EQUATE_2[1]] + res
            equations["mod_equate_2"].append(eq)
        elif bbl_len == EQUAL_2[0]:
            eq = eq[:EQUAL_2[1]] + res
            equations["equal_2"].append(eq)
    return equations

There were in total 8 different constraints applied on the input bytes, which was added to z3. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def set_idx(set_to):
    for i in set_to:
        s.add(f[i[0]] == i[1])

def sub2(s_list):
    for i in s_list:
        s.add(f[i[1]] - f[i[0]] == i[2])

def add2(a2_list):
    for i in a2_list:
        s.add(f[i[0]]+f[i[1]] == i[2])

def add3(a3_list):
    for i in a3_list:
        s.add(f[i[0]]+f[i[1]]+f[i[2]] == i[3])

def equate3(e3_list):
    for i in e3_list:
        res = (f[i[2]]*f[i[1]])%0x7fff
        s.add((f[i[0]]*res)%0x7fff == i[3])

def equate4(e4_list):
    for i in e4_list:
        res = (f[i[3]]*f[i[2]])%0x7fff
        res = (f[i[1]]*res)%0x7fff
        s.add((f[i[0]]*res)%0x7fff == i[4])

def mod_equate2(m2_list):
    for i in m2_list:
        s.add((f[i[1]] % f[i[0]]) * (f[i[0]] % f[i[1]]) == 0)
        s.add(f[i[0]] != f[i[1]]) 
        s.add(UDiv((UDiv(f[i[1]], f[i[0]]) + UDiv(f[i[0]], f[i[1]])),1) == i[2])

def distinct_add():
    for i in off:
        s.add(f[i[0]] != f[i[1]])

Running the script gives us the disassembly, and the extracted constraints

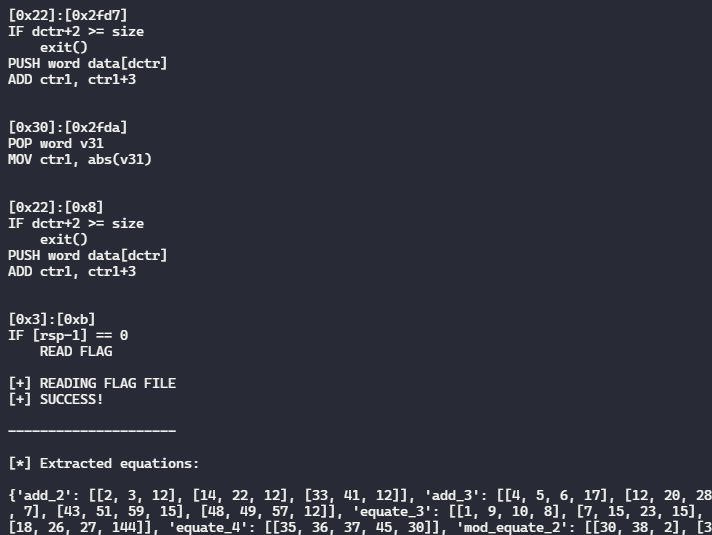
and pasting the extracted constraints to z3, gives us the input to be given,

pB738150rHt60714NP501s92420G3xUY013;Wo{=69h42Ob736B1y{@?1047uw`6

Sending this over the given nc connection, gives us the flag,

Flag: flag{kenken_is_just_z3_064c4}

Links to required files,
2k Disassembler Script - 2k_disassembler.py
Helper Script - helper.py
z3 solver script - z3_solver.py

Linux VM Reversing

1 / 2