Signal VM de1ta (Part 2) - de1CTF 2019

R3x
2019-08-09
Reversing / Linux

tl;dr

  • Challenge is a VM implemented over signals and ptrace
  • Reverse Instruction types and implementation
  • Use gdb scripting to find the executed code and get the pseudo VM code
  • Find out the algorithm (Max triangle sum) from VM instructions
  • Find an more optimized way to solve the problem (Or lazy solve it!).

Challenge Points: 769
Challenge Solves: 7
Solved by: R3x

Initial Analysis

Initial analysis shows us that there are minor changes between this binary and the signal_vm binary - in the way the VM works. Please refer to the writeup of signal_vm for learning about the VM structure.

VM structure

In the first stage of the challenge - we had access to all of the VM registers since they were all in the parent itself. Now in signal_vm_de1ta they are all in the memory space of the child - This makes it hard for us to track what is happening in the VM since we aren’t able to directly view its memory or registers.

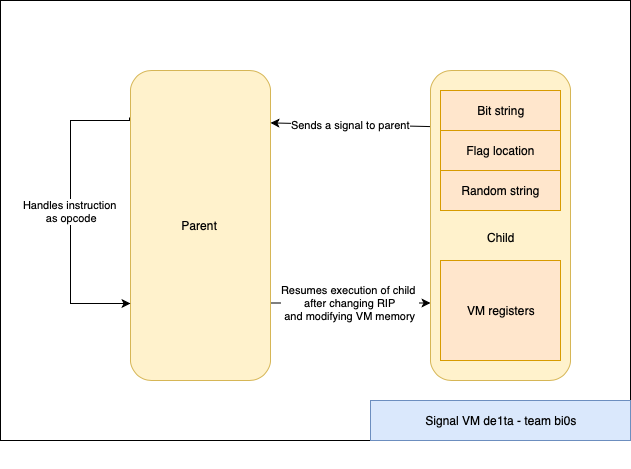
The VM uses the same four signals (SIGTRAP, SIGILL, SIGSEGV and SIGFPE) to serve as instruction classes. However there are a few significant differences from the first stage.

The VM(parent) uses PTRACE_PEEKDATA and PTRACE_POKEDATA to read and write data into the child memory which contains the memory and the registers.

Retrieving VM instructions

We tweaked the script for the old challenge to work for this one. Since we don’t have the register and memory states this time as that happens in the child, we decided to go ahead and write our own code to parse the instructions. So we were able to predict the contents of the VM registers accurately which helped us in figuring out what the child did.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
import gdb
import struct

class Regs(object):
    reg = [0] * 10
    eflags = 0
    flag = [48] * 0x80 + [0] * 0x100 + [10] * 5050

    def __repr__(self):
        final = "-------------------\n"
        for i in range(len(self.reg)):
           final += "\tRegister "+str(i)+" : "+str(self.reg[i]) + " | " + hex(self.reg[i]) + "\n"
        final += "\tEflags = " + str(self.eflags) + " | " + hex(self.eflags) + "\n"
        final += "\tFLAG = [[ " + "".join(map(chr, self.flag[:102])) + "]]\n"
        final += "------------------\n"
        return final

    def copy_reg(self, i, j):
        if i < 10:
            self.reg[i] = self.reg[j]
        else:
            self.eflags = self.reg[j]

    def copy_val(self, i, data):
        if i < 10:
            self.reg[i] = data
        else:
            self.eflags = data
    
    def flag_to_reg(self, src, dest):
        self.reg[src] = self.flag[self.reg[dest]]

    def reg_to_flag(self, src, dest):
        self.flag[self.reg[src]] = self.reg[dest]
        
    def operation(self, src, op, dest):
        self.reg[src] = eval("%d %s %d" % (self.reg[src], op , dest))
   
    def operation_reg(self, src, op, dest):
        self.reg[src] = eval("%d %s %d" % (self.reg[src], op ,self.reg[dest]))

    def update_eflag(self, dest, const):
        self.eflags = self.reg[dest] - const        

    def update_eflag_reg(self, dest, othreg):
        self.eflags = self.reg[dest] - self.reg[othreg]

class Opcode:
    opcode = ""
    val1 = 0
    const = 0
    src = 0
    dest = 0
    final = 0
    final2 = 0
    
    def __init__(self, opcode):
        self.opcode = opcode
        test = struct.unpack("<Q", int(opcode, 16).to_bytes(8, byteorder='big'))[0]
        self.val1 = test >> 56
        self.const = (test >> 48) & 0xff
        self.src = (test >> 40) & 0xff
        self.dest = (test >> 32) & 0xff
        self.final = struct.unpack("<I", ((test & 0xffffffff00) >> 8).to_bytes(4, byteorder='big'))[0]      
        self.final2 = struct.unpack("<I", (test & 0xffffffff).to_bytes(4, byteorder='big'))[0]

    def __repr__(self):
        str_out = "-------------------\n"
        str_out += "OPCODE : %s  |  %d\n" % (self.opcode, int(self.opcode, 16) ) 
        str_out += "val1 = %d | const = %d | src = %d | dest = %d\n" % (self.val1, self.const, self.src, self.dest)
        str_out += "val1 = %s | const = %s | src = %s | dest = %s\n" % (hex(self.val1), hex(self.const), hex(self.src), hex(self.dest))
        str_out += "final = %d    |   final2 =  %d \n" % (self.final, self.final2)
        str_out += "-------------------\n"
        return str_out
        

sig = {4: "SIGILL", 5 : "SIGTRAP", 8: "SIGFPE", 0xb: "SIGSEGV" }
mov_ins = {0: "%d: mov r%d r%d\n",1: "%d: mov r%d 0x%x\n" ,2: "%d: mov r%d [r%d]\n", 32: "%d: mov [r%d] r%d\n"}
ops = ["add" , "sub" ,  "mul" , "div" , "mod" , "or" , "and" , "xor" , "lsh" , "rsh"]
op_sym = ["+", "-", "*", "/", "%", "|", "&", "^", "<<", ">>"]
str_ops = ["%d: %s r%d r%d\n", "%d: %s r%d 0x%x\n"]
jmp = ["", "eq", "neq", "le", "lt", "ge", "gt"]

f = open('ins.out', 'w')

gdb.execute("file signal_vm_de1ta")
gdb.execute("set pagination off")
gdb.execute("b * 0x400CB2")
gdb.execute("b * 0x0400CB9")
gdb.execute("b * 0x0400CEC")
gdb.execute("b * 0x401062")

gdb.execute("r")
regs = Regs()

for i in range(20000):
    opcode = gdb.execute("p/x $rax", to_string=True).split("=")[1].strip()
    gdb.execute("c")

    sig = gdb.execute("p/x $al", to_string=True).split("=")[1].strip()
    gdb.execute("c")

    op = Opcode(opcode)    
    print(op)

    if int(sig, 16) == 5:
        opcode = gdb.execute("p/x $rax", to_string=True).split("=")[1].strip()
        gdb.execute("c")
        new_op = Opcode(opcode)

        if new_op.const == 1:
            f.write(mov_ins[new_op.const] % (i, new_op.src, new_op.final))
        else:
            f.write(mov_ins[new_op.const] % (i, new_op.src, new_op.dest))

        if new_op.const == 1:
            regs.copy_val(new_op.src, new_op.final)
        elif new_op.const == 0:
            regs.copy_reg(new_op.src, new_op.dest)
        elif new_op.const == 2:
            regs.flag_to_reg(new_op.src, new_op.dest)
        elif new_op.const == 32:
            regs.reg_to_flag(new_op.src, new_op.dest)
        else:
            f.write("\n ############ERROR################ \n")

        #f.write(new_op.__repr__())

    elif int(sig, 16) == 4:
        opcode = gdb.execute("p/x $rax", to_string=True).split("=")[1].strip()
        gdb.execute("c")
        new_op = Opcode(opcode)

        if new_op.const == 1:
            f.write(str_ops[1] % (i, ops[new_op.val1], new_op.src, new_op.final))      
        else:
            f.write(str_ops[0] % (i, ops[new_op.val1], new_op.src, new_op.dest))      

        if new_op.const == 1:
            regs.operation(new_op.src, op_sym[new_op.val1], new_op.final)
        else:
            regs.operation_reg(new_op.src, op_sym[new_op.val1], new_op.dest)
        
        #f.write(new_op.__repr__())

    elif int(sig, 16) == 8: 
        if op.src == 1:
            f.write("%d: cmp r%d 0x%x\n" % (i, op.dest, op.final2))
        else:
            f.write("%d: cmp r%d r%d\n" % (i, op.dest, op.final2 & 0xff))

        if op.src == 1:
            regs.update_eflag(op.dest, op.final2)
        else:
            regs.update_eflag_reg(op.dest, op.final2 & 0xff)
        
        #f.write(op.__repr__())

    elif int(sig, 16) == 0xb:
        f.write("%d: jmp %s 0x%x\n" % (i, jmp[op.src], op.dest))
        
        #f.write(op.__repr__())

    else:
        print("Error")

    #f.write(regs.__repr__())

Reversing the VM instructions

This was probably the most complicated VM algorithm I have seen in CTFs. I have written the python version of the code below - you can take a look at it.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

bit_string = [48] * 100
random_array = [..] # Huge array in the memory
flag = [0] * 100
max_sum = 0
while True:
    y = 0
    temp_array = []
    
    # Find the sum of the random array based on the
    # bit string.
    for x in range(len(bit_string)):
        temp_array.append(random_array[y + (x * (x + 1) >> 1)])
        if bit_string[x] == 49:
            y = y + 1

    # If the sum is greater than the max sum then copy
    # it to the flag location. 
    if sum(temp_array) > max_sum:
        max_sum = bit_sum
        for i in range(len(temp_array)):
            flag[i] = temp_array[i]

    ctr = 0
    flag = True

    # Increment the bit string value
    while flag:
        if bit_string[ctr] == 48:
            flag = False
        bit_string[ctr] = bit_string[ctr] ^ 1

Looking a bit deeper into the algorithm we see that it is actually taking the numbers in a very specific order.

x z = ((x * (x + 1)) >> 1) range of y + z
0 0 0
1 1 1..2
2 3 3..5
3 6 6..9
4 10 10..14
… … …
100 5050 5050..5150

From this order we figured out that this was basically dividing the array in form of a triangle and then trying to find the path which has the maximum sum.

Now we know what the VM is trying to do and it is taking a long time since the VM is trying to bruteforce the path. Now all we need to do is to find a more efficient way to solve this.

lazy solve

Since it is copying the path that has the maximum sum. I printed out the entire array in the form of a triangle and then I searched for the flag format manually - that is de1ctf{ and then I followed it until I reached the end.

You can probably trace - ~triangle~is from the above screen shot. That was like a wrapper around the flag.

flag was de1ctf{no~n33d~70-c4lcul473~3v3ry~p47h}

Intended Solution

After talking to the admin at the end of the CTF I learned that this was a DP problem and the solution was pretty simple.

You can take a look at the problem statement and the solution techniques here.

 Previous

Exploitation VM-Escape CVE-Writeups