Halloween Party - ASIS CTF Quals 2019

tl;dr

1. Find Elliptic Curve parameters from given points on the curve
2. Find x-coordinate of 2*P, given y-coordinate of 2*P
3. Invert 2 over mod (P.order()) and multiply the result with 2*P to get P
4. Submit ASIS{P.x} as the flag

Challenge Points: 182
Challenge Solves: 20
Solved by: s0rc3r3r, v3ct0r, v4d3r

In case you are new to Elliptic Curves, you can read about them in my library here

Preliminary Analysis

We are given a script that implements a basic Elliptic Curve (Weierstraas model)
$ y^2 \equiv x^3 + a*x + b\mod p $:

#!/usr/bin/env python

from fastecdsa.curve import Curve
from fastecdsa.point import Point
from Crypto.Util.number import *
from secret import EC_params, flag, Q


p, a, b, q, Px, Py = EC_params
C = Curve('halloween', p, a, b, q, Px, Py)
P = Point(Px, Py, curve = C)
P1 = Point(p + 1, 467996041489418065436268622304855825266338280723, curve = C)
P2 = Point(p - 1, 373126988100715326072483107245781156204485119489, curve = C)
P3 = Point(p + 3, 245091091146774561796627894715885724307214901148, curve = C)

assert (2*P).x == Q.x
assert bytes_to_long(flag) == P.x
assert ((-1) * Q).y == 621803439821606291947646422656643138592770518069

The script is importing EC parameters from a secret file, hence our first task becomes recovering the
Elliptic Curve parameters.

Notice that we are given three points on the curve: P1, P2 and P3, coordinates of which are known to us.
We can use these points to get the values of curve parameters.

Retrieving EC parameters

Let $ P1 = (x_1, y_1) $, $ P2 = (x_2, y_2) $ & $ P3 = (x_3, y_3) $
This implies:
$ y_1^2 = x_1^3 + a*x_1 + b \mod p $
$ y_2^2 = x_2^3 + a*x_2 + b \mod p $
$ y_3^2 = x_3^3 + a*x_3 + b \mod p $

Substituting values of P1 = (x₁, y₁), P2 = (x₂, y₂) & P3 = (x₃, y₃) and solving for a, b, p, we get:

p = 883097976585278660619269873521314064958923370261
b = 433481663214462017150295835098295925800218140157
a = 48029713913392144447486256568923103286673283937

Observations related to the curve

There are a few assertions in the challenge script:

assert (2*P).x == Q.x
assert bytes_to_long(flag) == P.x
assert ((-1) * Q).y == 621803439821606291947646422656643138592770518069

As one can see, our goal is to find the x-coordinate of P, which is the flag.

It is given that x-coordinate of P’ = 2*P (scalar multiplication) is equal to x-coordinate of Q. Note, this can
only happen when y-coordinate of Q is an additive inverse of y-coordinate of P’.

Let us try to understand the reason behind the above:

1. Consider an Elliptic Curve $ y^2\equiv x^3 + a*x + b\mod p $,
2. If two points A = (x₁, y₁) and B = (x₂, y₂) have same x-coordinate, then we can write:
   • $ y_1^2 \equiv c\mod p $
   • $ y_2^2 \equiv c\mod p $
3. Provided y₁ != y₂, we can say that $y_1 \equiv -y_2 \mod p$ as:
   • $ y_1^2 \equiv (-y_2)^2 \equiv c\mod p$

We are given y-coordinate of (-1)*Q, which implies that we are given the y-coordinate of P’

On the basis of observations above, we can draw the Elliptic Curve and mark relevant points: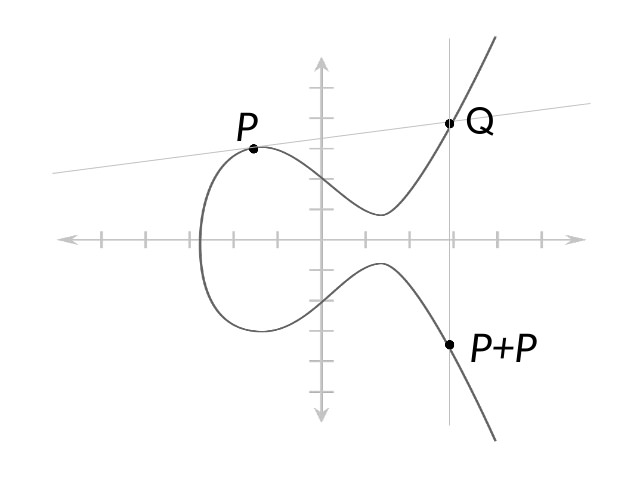

Note that the above diagram is made for Curve over $\mathbb{R}$, whereas our Curve is defined over $GF(p)$,
but the idea remains the same! Also, $ P+P == 2*P $

Finding x-coordinate of Q

Provided y-coordinate of a point on the curve, we can compute it’s corresponding x-coordinate by finding
solutions of the equation: $ x^3 + a*x + (b-y^2) \equiv 0 \mod p $

Values of a, b, p in our challenge are as follows:

a = 48029713913392144447486256568923103286673283937
b = 433481663214462017150295835098295925800218140157
p = 883097976585278660619269873521314064958923370261

We computed the x-coordinate of Q by running the following function in Mathematica:

Solve[x^3 + 48029713913392144447486256568923103286673283937 x + 837637963235166117552443765282645351326329278968 == 0, x, Modulus ->883097976585278660619269873521314064958923370261]

Alternatively, you can also use roots() in sagemath:

a = 48029713913392144447486256568923103286673283937
b = 433481663214462017150295835098295925800218140157
p = 883097976585278660619269873521314064958923370261

P.<X> = PolynomialRing(GF(p))
f=X^3+a*X+b-Qiy^2
Qix=f.roots()[0][0]

Source: HATS SG team’s solution script - https://pastebin.com/cUAa6R9W

Recovered x-coordinate of Q as: 708927573459527177103235542148826237228344428002
Since x-coordinate of Q and that of P’=2*P is the same, we have both x and y-coordinates of P’.

Knowledge of both coordinates of 2*P would be adequate to get coordinates of P

Finding x-coordinate of P

Let the order of subgroup generated by P be ord_P. We can then write:
$ 2*P = P’ $
$ P = ({2^{-1}\mod ord_P})*P’ $

But, how do we find order of subgroup generated by P?

We know from Lagrange’s Theorem that order of the subgroup generated by a point P on the curve is a factor of cardinality of the curve.

But if P is a generator, then order of the subgroup generated by P is exactly equal to the cardinality of
the curve. We can find out cardinality of a curve E using the following function in sagemath:

E.cardinality()

Cardinality of our curve has several factors: [3, 5, 13, 257, 134021890447, 97090721460179,
1354215209508238123] and order of P can be a factor of combination of any of these factors.

But we went on further anyway, assuming that P is a generator for the curve given in this challenge and got
the correct coordinates :)

You can read the full solution script here:

from Crypto.Util.number import *
from sage.all import *

y1 = 467996041489418065436268622304855825266338280723
y2 = 373126988100715326072483107245781156204485119489
y3 = 245091091146774561796627894715885724307214901148

b = 433481663214462017150295835098295925800218140157
a = 48029713913392144447486256568923103286673283937
p = 883097976585278660619269873521314064958923370261
E = EllipticCurve(GF(p), [a, b])
P1 = E((p+1, y1))
P2 = E((p-1, y2))
P3 = E((p+3, y3))

Q_y = -621803439821606291947646422656643138592770518069 % p
_2P_y = 621803439821606291947646422656643138592770518069

# Use Mathematica to solve, sagemath's solve_mod shows overflow
# Solve[x^3 + 48029713913392144447486256568923103286673283937 x + 837637963235166117552443765282645351326329278968 == 0, x, Modulus ->883097976585278660619269873521314064958923370261]
Q_x = 708927573459527177103235542148826237228344428002L
_2P_x = Q_x

Q = E((Q_x, Q_y))
_2P = E((_2P_x, _2P_y))
print Q
print "\n"
print _2P

assert _2P[0] == Q[0]

list1 = [3, 5, 13, 257, 134021890447, 97090721460179, 1354215209508238123]
_cardinality = reduce(lambda i, j: i*j, list1)

tP = inverse_mod(2, _cardinality)*_2P
if 2*tP == _2P:
    print "Voila! P:", tP

On running the above code, we got the coordinates of P as: (804028439497151963978256498500182891314861988389, 272052071247970914287181631972199909106801861256)

Flag: ASIS{804028439497151963978256498500182891314861988389}

In case of any query, feedback or suggestion, feel free to comment or reach me out on Twitter!